Advanced Research Laboratory for Multifunctional Lightweight Structures (ARL-MLS) Computational Mechanics

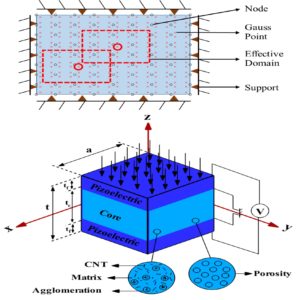
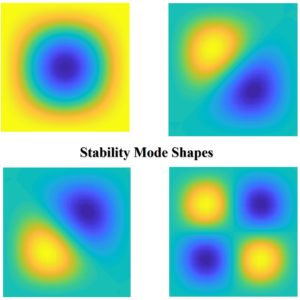
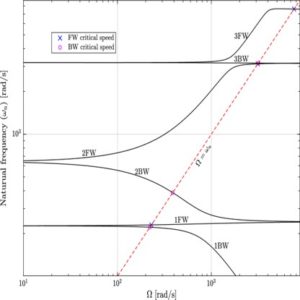
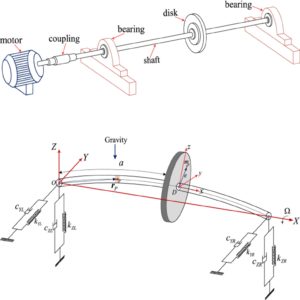
Research in Computational Mechanics

Problem Statement

At ARL-MLS, current and advancing trends in numerical, analytical and experimental investigations are bridged to develop novel and innovative computational methods to overcome pressing challenges in the field of aerospace, biomedical, material sciences and electro-mechanical engineering. Highly advanced and precise nonlinear, dynamic and multiscale computational models are proposed to further explore and discover design alternatives. Moreover, cost effective surrogate methods are developed incorporating technological trends such as Machine Learning, Artificial Intelligence, Meshless and other innovative approaches to address the short comings of traditional ones. ARL-MLS strives to come up with efficient solutions for the following challenges:

Computational cost-effective approaches to treat different types of mechanical analyses.
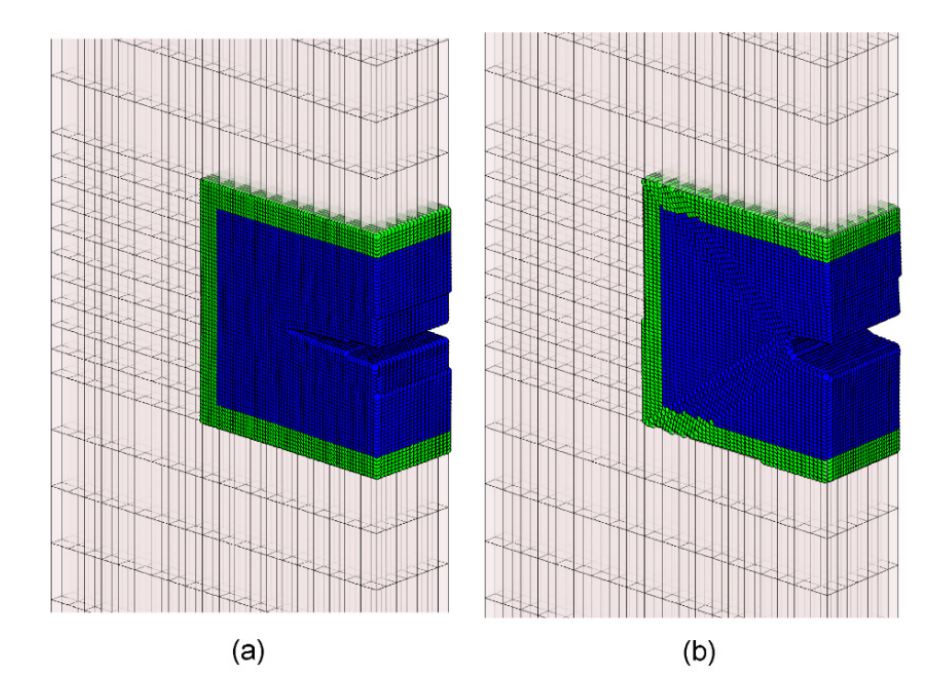
Circumventing current obstacles in Finite Element Methods (FEMs) such as modeling cracks, breaking into smaller parts and large deformations.
Enhance solution accuracy of engineering problems to deal with varying scales while managing computational costs.
Methods for modeling complex systems while considering the effects of coupled members while minimizing computational efforts.
Component level enhancements of high-tech machines while incorporating true parameters and eliminating redundancies.
Integration of numerical models with simulation workflows for higher control over system definition.
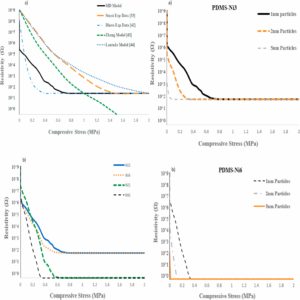
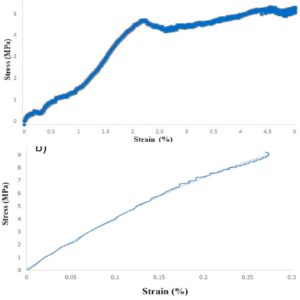
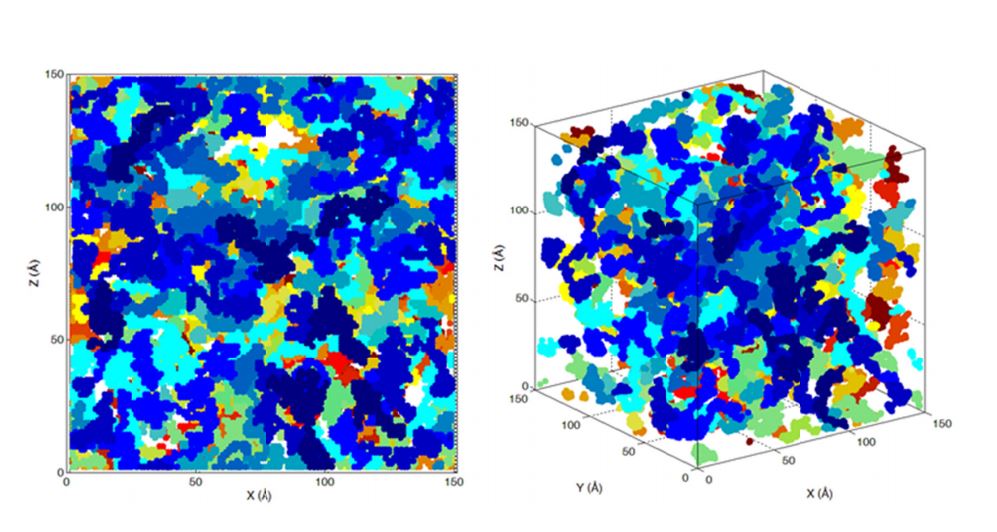
Alternatives for material characterization of composites/nanocomposites while overcoming the need of experimental tests.

Solutions

To overcome the many global challenges in the field of Computational Mechanics, ARL – MLS has been actively developing cutting edge solutions such as:

Developing advanced FEM and meshless approach for mechanical analyses of novel structures.
Applying mesh-free methodology and bridging methods to rectify concerns caused by conventional FEMs or analytical approaches.
Proposing and applying cutting edge multiscale methods for characterizing crack growth, interface vicinity of two materials with different scales and porous materials.
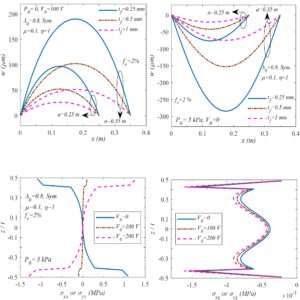
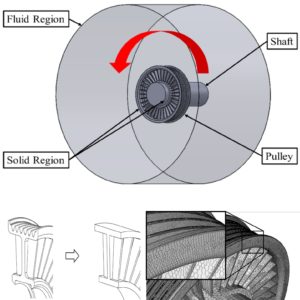
Providing computationally efficient and easy to apply multi-DOF methods to investigate dynamics of high-tech components with complex geometries.
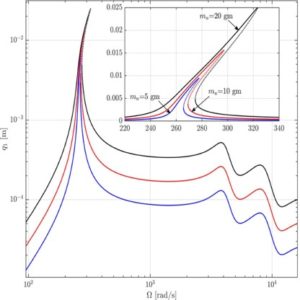
Offering highly precise analytical solutions for dynamic behaviors of high-speed machines considering nonlinearities.
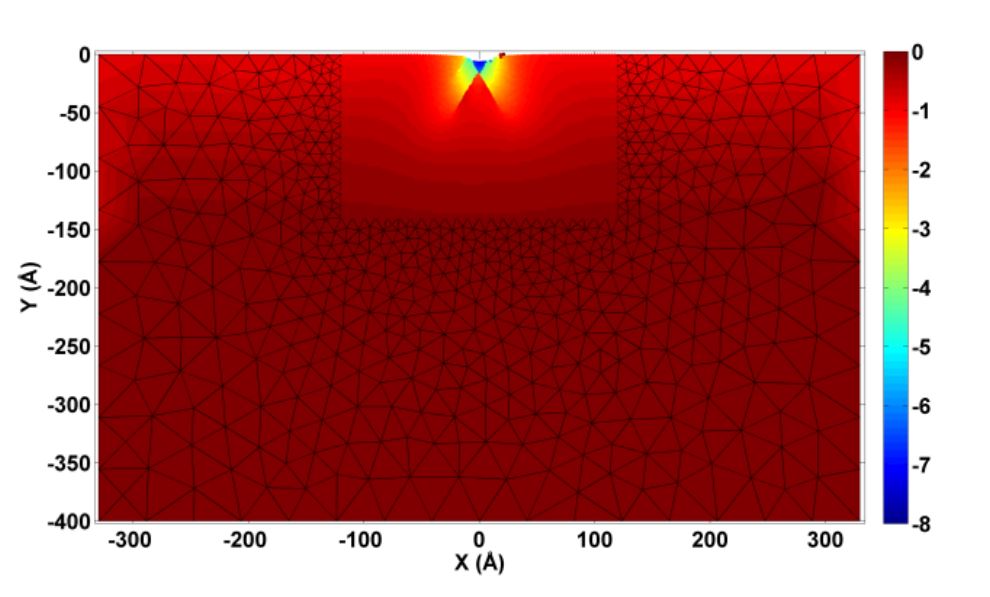
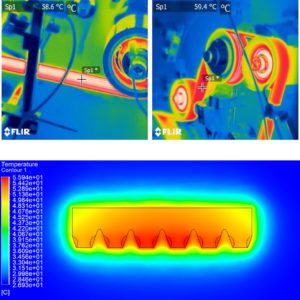
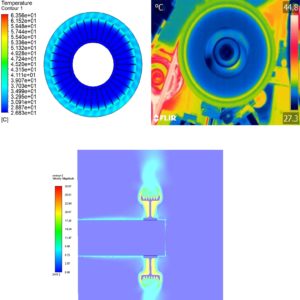
Developing reliable physics‐based scalarization methods to process 2D models instead of 3D simulations.
Providing innovative computationally effective and fast analytical approaches to study acoustic, thermal and mechanical behaviors of critical industrial elements.
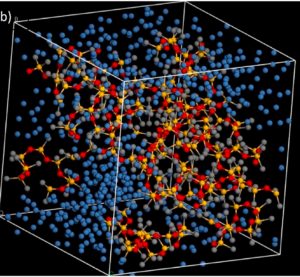
Performing atomistic analysis to characterize unconventional nanocomposite materials.

Projects

A molecular dynamics study of electro-mechanical properties of conductive nanocomposites

Abstract

Molecular dynamics was applied to develop a novel PDMS and PDMS-Ni nanocomposite model. First, the PDMS model was validated in terms of the elastic and compressive moduli using available experimental data. The model was then used as a benchmark to add Ni nanoparticles and create a PDMS-Ni conductive nanocomposite model. This model was studied under uniaxial tensile and compressive loading conditions for different Ni filler ratios and mean particle diameters. The electrical resistivity of the model was then obtained as a function of pressure and the compressive stresses. The PDMS-Ni MD model was validated via the literature and shown to successfully predict electrical resistivity variations versus compressive stresses. The results show that as the Ni filler ratio increased from 3:1 to 6:1, the drop in initial electrical resistivity of the composites occurred much faster and at lower stresses. Furthermore, as the mean Ni particle diameter size was increased from 1 nm to 5 nm, the electrical conductivity of the PDMS-Ni improved at different filler ratios. The developed PDMS-Ni MD model can be used to study the electrical and mechanical behaviors of such materials in biosensor applications. It can further be used to study the effects of adding other fillers to PDMS matrix.

Citation

SMM Zamani, K Behdinan, A molecular dynamics study of the mechanical and electrical properties of Polydimethylsiloxane-Ni conductive nanocomposites, Composites Science and Technology, 200, 2020, 108463,

Available: https://doi.org/10.1016/j.compscitech.2020.108463

Developing mesh-free solutions for thermo-electro-mechanical responses of novel engineering structures

Abstract

In this paper, a meshless method has been developed to analyze stresses and deflections in an advanced smart lightweight sandwich plate (ASLSP) subjected to thermo-electro-mechanical loads. In ASLSP, a passive sandwich plate consisting of a lightweight porous core and two graphene nanocomposite layers is integrated between two active piezoceramic faces. Moreover, functionally graded profiles have been considered for the dispersions of porosity and graphene in their corresponding layers. In the meshless method, MLS shape functions has been utilized, and essential boundary conditions are implemented using transformation approach. A version of Halpin-Tsai equations capable of capturing nanoscale effects of randomly oriented graphene is adopted to approximate the temperature dependent mechanical properties of graphene nanocomposite layers. The highly coupled governing equations are extracted by minimizing total energy function obtained from the estimation of displacement domain with Reddy's third order plate theory called TSDT). The influences of different aspects of ASLSP including loading, graphene content, porosity and geometric details have been studied on thermo-electro-mechanical stresses and deflections. It is observed that both graphene content and dispersion profile have considerable influence on ASLSP's deflections. Moreover, embedding pores in core layer offers a significant reduction in structural weight and a considerable stability in structural bending stiffness.

Citation

Moradi-Dastjerdi R, Behdinan K. Thermo-electro-mechanical behavior of an advanced smart lightweight sandwich plate. Aerosp Sci Technol 2020;106:106142.

Available: https://doi.org/10.1016/j.ast.2020.106142.

Nonlinear vibrations of high-speed rotor systems using a flexible and viscoelastic models

Abstract

In this paper, the three-dimensional nonlinear dynamics and force transmissibility characteristics of a flexible shaft-disk rotor system are investigated numerically. The rotor system is comprised of a flexible shaft supporting a rigid disk, and the shaft ends are mounted on viscoelastic elements (bearing/support). The dynamic model of the system is developed considering the coupled axial and bending–bending elastic motions of the shaft while the disk is modeled as a rigid body. The equations of motion (EOM) obtained using Lagrange’s equation are discretized using the assumed mode method utilizing large number of modes to examine the system dynamics accurately for multiple resonance regions. The EOM are then linearized to obtain the natural frequencies to construct the Campbell diagrams and investigate the influence of the bearing stiffness and disk location on critical speeds and whirling modes. The harmonic balance method combined with the pseudo-arclength continuation method is used to construct the nonlinear frequency response and force transmissibility curves due to disk unbalance force. The effects of the bearing stiffness and damping, unbalance force magnitude and disk location on the nonlinear multi-mode primary frequency response and force transmissibility are then thoroughly investigated.

Citation

Al-Solihat, M.K., Behdinan, K. Nonlinear dynamic response and transmissibility of a flexible rotor system mounted on viscoelastic elements. Nonlinear Dyn 97, 1581–1600 (2019).

Available: https://doi.org/10.1007/s11071-019-05078-3

A Bridging Cell Multiscale Methodology to Model the Structural Behaviour of Polymer Matrix Composites

Abstract

Composite and nanocomposite materials exhibit behaviour which is inherently multiscale, extending from the atomistic to continuum levels. In composites, damage growth tends to occur at the nano and microstructural scale by means of crack growth and fibre-matrix debonding. Concurrent multiscale modeling provides a means of efficiently solving such localized phenomena, however its use in this application has been limited due to a number of existing issues in the multiscale field. These include the seamless transfer of information between continuum and atomistic domains, the small timesteps required for dynamic simulation, and limited research into concurrent multiscale modeling of amorphous polymeric materials. The objective of this thesis is thus twofold: to formulate a generalized approach to solving a coupled atomistic-to-continuum system that addresses these issues and to extend the application space of concurrent multiscale modeling to damage modeling in composite microstructures. To achieve these objectives, a finite element based multiscale technique termed the Bridging Cell Method (BCM), has been formulated with a focus on crystalline material systems. Case studies are then presented that show the effectiveness of the developed technique with respect to full atomistic simulations. The BCM is also demonstrated for applications of stress around a nanovoid, nanoindentation, and crack growth due to monotonic and cyclic loading. Next, the BCM is extended to modeling amorphous polymeric material systems where an adaptive solver and a two-step iterative solution algorithm are introduced. Finally, the amorphous and crystalline BCM is applied to modeling a polymer-graphite interface. This interface model is used to obtain cohesive zone parameters which are used in a cohesive zone model of fibre-matrix interfacial cracking in a composite microstructure. This allows for an investigation of the temperature dependent damage mechanics from the nano to microscale within polymer matrix composites due to transverse loading. Results from the simulations indicate that the BCM creates a seamless coupling between continuum and atomistic domains for crystalline material systems while substantially reducing force imbalance for amorphous material systems. Multiscale simulation results of the composite microstructure indicated that the model accurately predicted both quantitative (elastic modulus, strength, stress-strain response) and qualitative behaviour when compared to experimental results from the literature.

Citation

Iacobellis, V., & Behdinan, K. (2012). Multiscale coupling using a finite element framework at finite temperature. International journal for numerical methods in engineering, 92(7), 652-670.

An innovative model for the thermal behavior of belt drive systems

Abstract

Belt drive transmissions are widely utilized in and critical to aviation design. Thermal fatigue and deterioration inside a drive system must be avoided. To this end, this study develops an innovative thermal model for providing real-time temperature plots of belt drive systems operating under constant RPM conditions. This model analytically establishes a system of governing equations based on the thermal flow and exchange occurring in the system. The coefficient inside the thermal equation for each pulley and its variation curve are calculated using a numerical approach. The precalculated baseline numerical simulations are then stored in a database, and they are imported and modified analytically to calculate the temperature distribution across each pulley. Using this approach significantly reduces time-consuming numerical calculation. The resulting temperature plot is accurate and efficient. Experimental validation demonstrates the high reliability of the temperature predictions presented by this model under various operating conditions. Therefore, the proposed novel model can successfully be applied to applications involving high-reliability transmissions.

Citation

X. Liu and K. Behdinan, Modeling and Experimentation of Temperature Calculations for Betl Drive Transmission Systems in the Aviation Industry. Advanced Multifunctional Lightweight Aerostructures: Design, Development, and Implementation. 2021, pp. 123-149.

Available: https://doi.org/10.1002/9781119756743.ch7